Are you curious about regular polygons? In this article, we will delve into the world of polygons and explore their fascinating properties and characteristics. From the definition of a polygon to its various components and properties, we'll cover it all. Let's get started!
What Exactly is a Polygon?
A polygon is a two-dimensional enclosed figure formed by joining three or more straight lines. You can think of it as a "flat figure" with straight sides. For example, a square is a polygon made by joining four straight lines of equal length.
 Examples of polygons
Examples of polygons
The Parts of a Polygon
To understand polygons better, let's break them down into their three main components:
Sides
A side is a line segment that joins two vertices of a polygon.
Vertices
A vertex is the point where two sides of a polygon meet.
Angles
Polygons have both interior and exterior angles. The interior angles are formed within the enclosed surface of the polygon by joining its sides.
 Parts of a polygon
Parts of a polygon
Introducing Regular Polygons
When all the sides and interior angles of a polygon are equal, we refer to it as a regular polygon. Examples of regular polygons include squares and equilateral triangles. In regular polygons, not only are the sides congruent, but the angles are as well, making them equiangular.
 A regular polygon
A regular polygon
Exploring the Properties of Regular Polygons
Regular polygons exhibit some interesting properties that set them apart. Let's take a look at a few of these properties:
- All the sides of a regular polygon are equal.
- All the interior angles of a regular polygon are equal.
- The sum of the exterior angles of a regular polygon is always 360°.
Calculating the Perimeter of a Regular Polygon
Since a regular polygon has all sides equal, the perimeter is simply the sum of all its sides. For example, if the side of a regular polygon measures 6 cm and there are 5 sides, the perimeter would be 5 * 6 = 30 cm.
 A regular pentagon with a side length of 6 cm
A regular pentagon with a side length of 6 cm
The Sum of Interior Angles in a Regular Polygon
For a regular polygon with n sides, the sum of its interior angles can be calculated using the formula (n - 2) 180°. Let's say we have a regular polygon with 6 sides. The sum of its interior angles would be (6 - 2) 180° = 720°.
The Measure of Each Interior Angle of a Regular Polygon
Since a regular polygon is equiangular, each interior angle is of equal measure. For a regular polygon with n sides, each interior angle can be calculated using the formula (n - 2) 180° / n. Let's consider a regular polygon with 8 sides. Each interior angle would be (8 - 2) 180° / 8 = 135°.
 Angles in a regular octagon
Angles in a regular octagon
The Measure of Each Exterior Angle of a Regular Polygon
In a regular polygon, the sum of all exterior angles is always 360°. Therefore, the measure of each exterior angle of a regular polygon can be calculated as 360° / n, where n represents the number of sides.
Determining the Number of Diagonals of a Regular Polygon
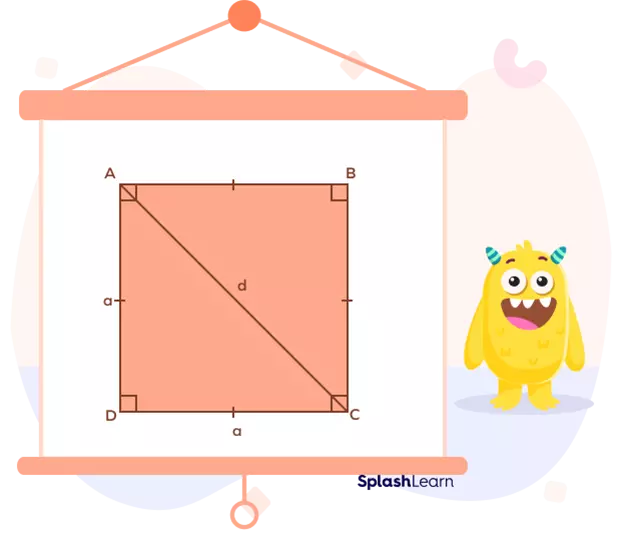
The number of diagonals in a polygon with n sides can be found using the formula n(n - 3) / 2. Each vertex of the regular polygon connects to (n - 3) vertices, and to avoid double counting, we divide the result by two. For example, a regular polygon with 4 sides (a square) has 2 diagonals.
 Diagonals of a square
Diagonals of a square
Counting the Number of Triangles in a Regular Polygon
If a regular polygon has n sides, the number of triangles formed by joining the diagonals from one corner of the polygon is equal to n - 2. For instance, a regular polygon with 4 sides forms 2 triangles.
 Number of triangles in a square
Number of triangles in a square
Analyzing the Lines of Symmetry in a Regular Polygon
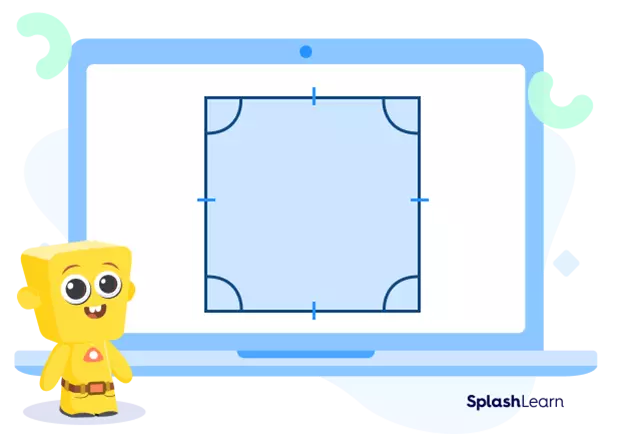
The line of symmetry in a shape is an axis or imaginary line that divides it into identical halves, passing through its center. Since all sides of a regular polygon are equal, the number of lines of symmetry is equal to the number of sides (n). For example, a square with 4 sides has 4 lines of symmetry.
 Lines of symmetry in a square
Lines of symmetry in a square
Understanding the Order of Symmetry in a Regular Polygon
A regular polygon has rotational symmetry when it can be rotated and still appear the same. The order of rotational symmetry in a regular polygon is equal to the number of sides (n). Additionally, the angle of rotational symmetry in a regular polygon can be calculated as 360° / n. For instance, a square has an order of rotational symmetry equal to 4, meaning that when rotated four times at an angle of 90°, it will retain its original appearance.
 Rotational symmetries of a square
Rotational symmetries of a square
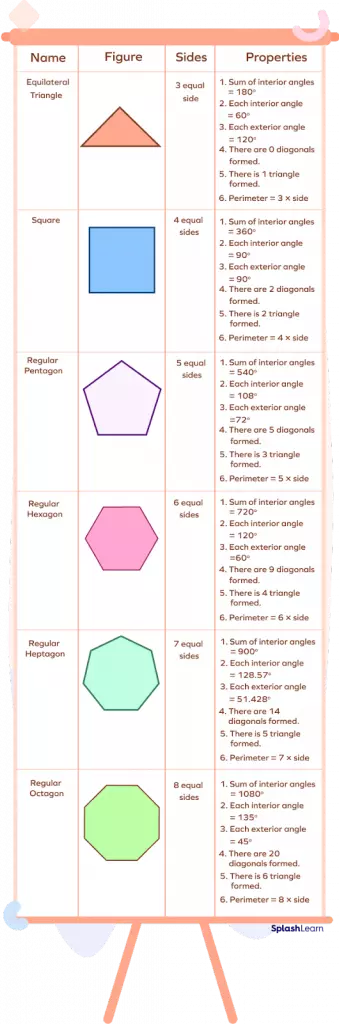
Exploring Different Regular Polygons
Here is a list of some common regular polygons:
- Equilateral Triangle
- Square
- Pentagon
- Hexagon
- Heptagon
- Octagon
- Nonagon
- Decagon
 Properties of regular polygons
Properties of regular polygons
Fun Fact!
Did you know that the sum of the exterior angles of any polygon, regular or irregular, is always equal to 360°? This intriguing fact holds true for all polygons!
Solved Examples on Regular Polygons
Let's tackle a few practice problems involving regular polygons to solidify our understanding:
Example 1: Find the number of diagonals of a regular polygon with 12 sides.
Solution: The number of diagonals in an n-sided polygon can be calculated using the formula n(n - 3) / 2. For a regular polygon with 12 sides, the number of diagonals would be 12 * (12 - 3) / 2 = 54.
Example 2: If each interior angle of a regular polygon measures 120°, what is the number of sides?
Solution: Using the formula for each interior angle: (n - 2) * 180° / n = 120°, we can solve for n. By simplifying the equation, we find that n = 6. Therefore, the number of sides in the regular polygon is 6.
Example 3: Can a regular polygon have internal angles measuring 100° each?
Solution: Each exterior angle of a polygon can be calculated as 180° - interior angle measure. In this case, each exterior angle would be 180° - 100° = 80°. However, the formula for each exterior angle, 360° / n, where n is the number of sides, leads to a decimal value for n. Thus, it is not possible for a regular polygon to have internal angles measuring 100° each.
Practice Problems and Frequently Asked Questions
Ready to test your skills? Try solving the practice problems and explore the frequently asked questions related to regular polygons.
Now that you've delved into the world of regular polygons, you possess a deeper understanding of their definition, properties, and characteristics. Remember, regular polygons are not only mathematically intriguing; they also play a significant role in various fields, including geometry, architecture, and art. Keep exploring and uncovering the wonders of polygons!












