Have you ever heard of a heptagon? A heptagon is a unique polygon that possesses seven sides and seven interior angles, making it a captivating shape to explore. In this article, we will delve into the intriguing world of heptagons, uncovering their properties, types, formulas, and more. Join me on this journey as we unravel the mysteries of heptagons together!
What exactly is a heptagon?
A heptagon is a closed, two-dimensional shape with precisely seven sides. The prefix "hepta-" comes from the Greek word for "seven," reflecting the number of sides in this intriguing polygon. In real-life, heptagons can be found in various contexts. For instance, the fifty pence and twenty pence coins in the UK are excellent examples of heptagons.
The Versatility of Heptagon Shapes
Heptagons come in various forms, each with its unique arrangement of sides and angles. Let's take a closer look at the different shapes a heptagon can assume.
The Distinction Between Regular and Irregular Heptagons
Heptagons can be classified into two main categories: regular and irregular. Additionally, heptagons can be further classified as concave or convex, based on the nature of their angles.
Regular Heptagons: The Epitome of Symmetry
A regular heptagon exhibits a harmonious balance between its sides and interior angles. In other words, all sides and angles of a regular heptagon are equal. Take a moment to appreciate the beauty of a regular heptagon in the image below:
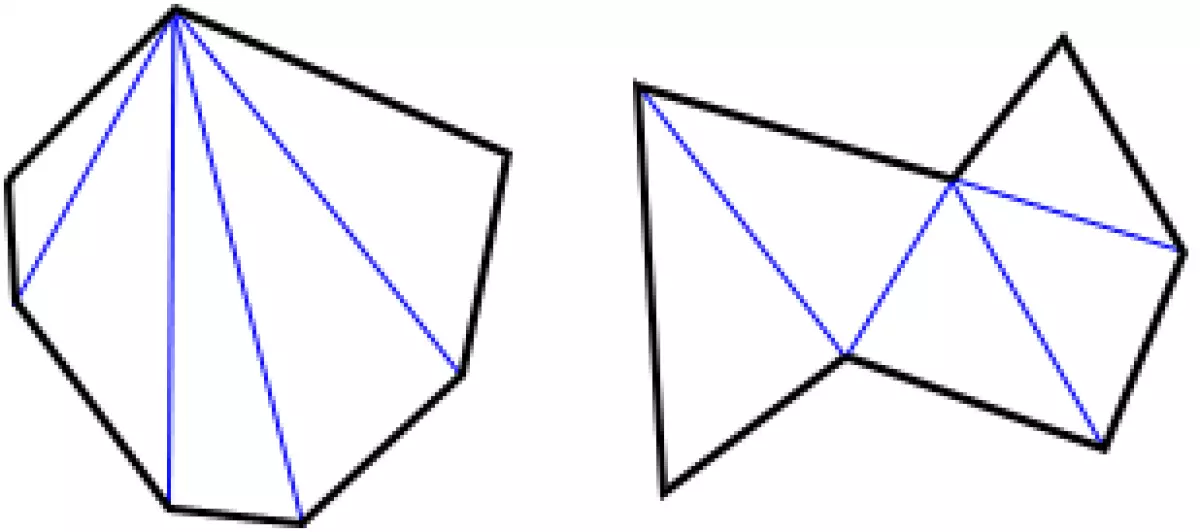Image: A captivating visual representation of a regular heptagon.
Distinctive Properties of Regular Heptagons
Let's explore some noteworthy properties of regular heptagons:
- The interior angles of a regular heptagon measure approximately 128.57° each.
- The exterior angles of a regular heptagon are approximately 51.43° each.
- A regular heptagon boasts seven congruent vertices and sides.
- It possesses seven lines of symmetry.
- Regular heptagons are always convex.
Irregular Heptagons: Embracing Uniqueness
Unlike their regular counterparts, irregular heptagons exhibit varying measurements of sides and interior angles. This diversification results in a unique and captivating appearance. Take a moment to observe an irregular heptagon:
Image: An intriguing representation of an irregular heptagon.
As you can see, not all sides and angles of an irregular heptagon are congruent, making it irregular. Furthermore, irregular heptagons can be either concave or convex.
Understanding Convex Heptagons
A convex heptagon refers to a heptagon in which all interior angles measure less than 180°. Consequently, all diagonals of a convex heptagon lie within the boundaries of the shape. It's important to note that while a regular heptagon is always convex, a convex heptagon can be either regular or irregular. Take a look at the example below to gain a clearer understanding:
Image: An illustration showcasing an irregular convex heptagon.
Notice that none of the interior angles measure greater than 180°. However, not all sides and interior angles are congruent, signifying its irregular nature.
Unveiling the Enigma of Concave Heptagons
Contrary to convex heptagons, concave heptagons possess at least one interior angle that measures greater than 180°. In concave heptagons, there are corresponding diagonals that extend beyond the boundaries of the shape. Due to the presence of an angle greater than 180°, concave heptagons are always irregular. Observe this fascinating example:
Image: An intriguing representation of a concave heptagon.
Note that two interior angles measure greater than 180°, confirming the concave nature of the heptagon.
Exploring the Fascinating Properties of Heptagons
Heptagons possess several intriguing properties that set them apart from other shapes. Let's take a closer look at these properties:
- Heptagons consist of seven sides, angles, and vertices.
- The sum of the interior angles of a heptagon equals 900°.
- The sum of the exterior angles of a heptagon equals 360°.
- A heptagon can be divided into five triangles.
- The number of diagonals in a heptagon is 14.
Unmasking the Formulas for Heptagons
To navigate the world of heptagons with ease, it's crucial to familiarize ourselves with the formulas associated with them. Below, you will find formulas for calculating the area, perimeter, measure of interior angles, and the sum of interior angles of a heptagon.
Area of a Heptagon
The formula for calculating the area of a regular heptagon is as follows:
A = (7/4) × a² × cot(π/7)
However, this formula can be simplified to:
A ≈ 3.634 × a²
Perimeter of a Heptagon
The formula for calculating the perimeter of a regular heptagon is:
P = 7a
Here, "a" represents the length of one side of the heptagon. For irregular heptagons, the perimeter is simply the sum of all the sides.
Measure of Interior Angles in a Heptagon
The formula to determine the measure of the interior angles in any regular polygon is:
Interior Angle = (n-2) × 180° / n
For a regular heptagon, the formula becomes:
Interior Angle ≈ 128.57°
Sum of Interior Angles in a Heptagon
To find the sum of the interior angles in any polygon, you can use the formula:
Sum of Interior Angles = (n-2) × 180°
For a heptagon, the sum of the interior angles equals 900°.
Understanding Heptagon Angles
In a heptagon, the sum of the interior angles amounts to 900°, while the sum of the exterior angles is 360°. In irregular heptagons, individual interior and exterior angles may vary. However, in a regular heptagon, each interior angle measures approximately 128.57°, while each exterior angle measures around 51.43°.
Revealing the Diagonals of a Heptagon
Diagonals play a crucial role in the structure of a heptagon. They are line segments that connect non-consecutive vertices. An intriguing characteristic of heptagons is that they possess fourteen distinct diagonals. Let's visualize this concept below:
Image: A representation illustrating the diagonals of a heptagon.
As depicted, there are four diagonals extending from each of the seven vertices of the heptagon, resulting in a total of 14 diagonals.
Unraveling the Symmetry of Heptagons
Regular heptagons exhibit remarkable symmetry, boasting seven lines of symmetry. Additionally, they possess rotational symmetry of order seven, meaning that they can be rotated seven times in a full 360° rotation while retaining their original shape. Marvel at the harmony of symmetry in regular heptagons!
In conclusion, heptagons are captivating polygons with their distinctive properties, types, and formulas. Whether you encounter heptagons in mathematical applications or stumble upon them in real-life objects, their allure is undeniable. Now that we have explored the enchanting realm of heptagons together, I hope you have gained a deeper appreciation for their beauty and complexity.
