Trong hình học, đa giác thập diện là một hình đa giác có mười cạnh hoặc 10 đỉnh. Tổng tổng các góc trong của một đa giác thập diện đơn giản là 1440°.
Đa giác thập diện đều
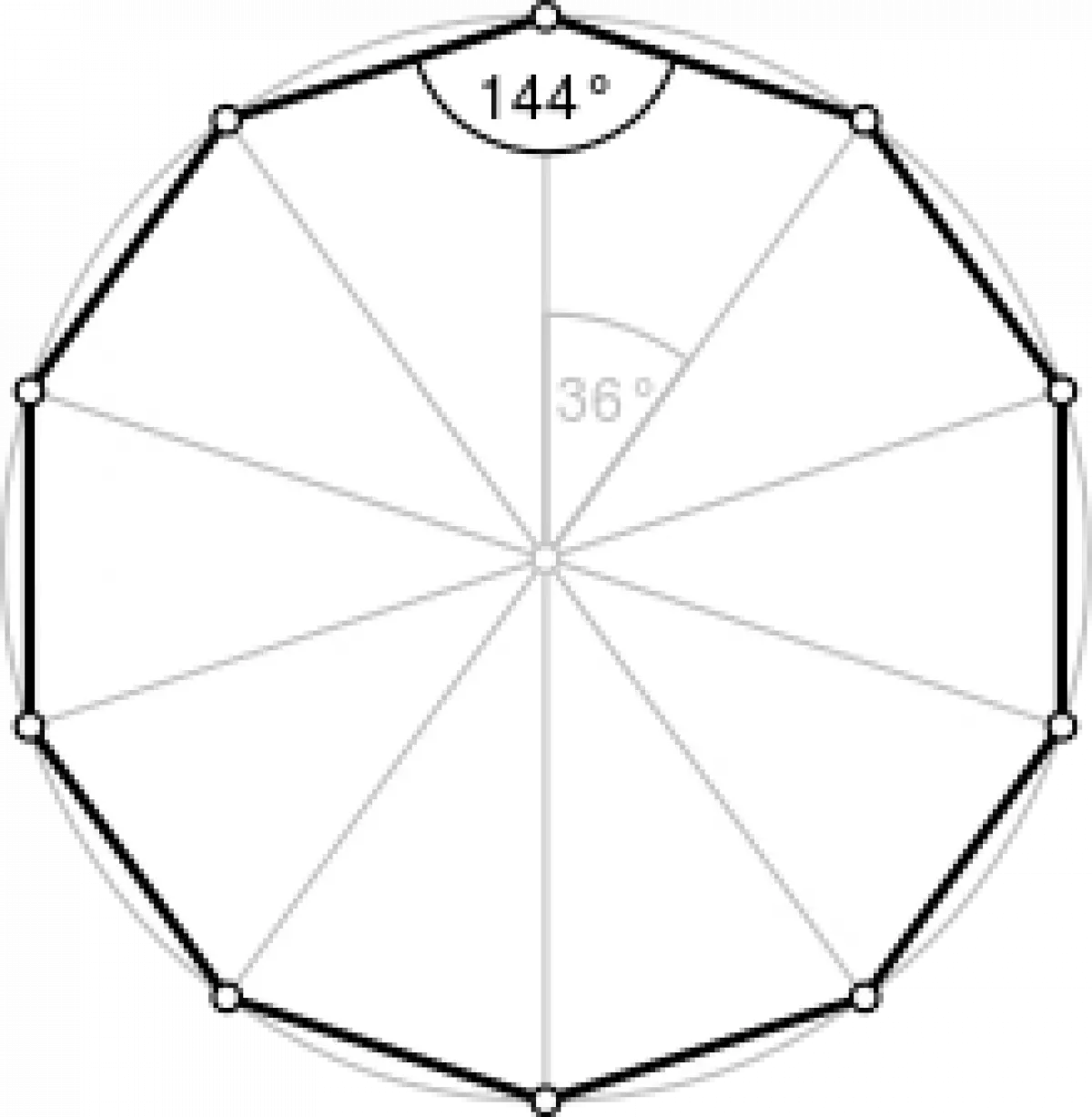
Một đa giác thập diện đều có tất cả các cạnh có độ dài bằng nhau và mỗi góc trong luôn bằng 144°. Ký hiệu Schläfli của nó là {10} và cũng có thể được xây dựng như một đa giác cắt giữa hai loại cạnh khác nhau.
Độ dài cạnh
Hình dạng dưới đây là một đa giác thập diện đều với độ dài cạnh a và bán kính R của đường tròn ngoại tiếp.
- Tam giác E10E1M có hai đường chéo bằng nhau có độ dài R và một đáy có độ dài a.
- Đường tròn xung quanh E1 với bán kính a gặp cắt [ME10] tại một điểm P.
- Tam giác E10E1P là một tam giác cân với đỉnh E1 và với các góc đáy m ∠E1E10P = m ∠E10PE1 = 72°.
- Vì vậy m ∠PE1E10 = 180° - 2 * 72° = 36°. Do đó, m ∠ME1P = 72° - 36° = 36° và do đó E1MP cũng là một tam giác cân với đỉnh P. Chiều dài hai cạnh của nó là a, vì vậy độ dài của [PE10] là R - a.
Các tam giác cân E10E1M và PEO có các góc bằng nhau là 36° tại đỉnh, do đó chúng tương tự nhau, do đó:
a / R = (R - a) / a
Nhân với các mẫu số R, a > 0 dẫn đến phương trình bậc hai:
a^2 = R^2 - aR
Phương trình này cho độ dài cạnh a có một nghiệm dương: a = R / 2 (- 1 + sqrt(5)). Vì vậy đa giác thập diện đều có thể được xây dựng với thước và compas.
Kết luận: R = 2a(5 - 1) và cạnh đáy của ΔE10E1M (tức là độ dài của [MD]) là h = R^2 - (a / 2)^2 = a^2(5 + 2√5) và tam giác có diện tích AΔ = a^2 * h = a^2/4(5 + 2√5).
Diện tích
Diện tích của một đa giác thập diện đều với độ dài cạnh a được xác định bởi: A = (5/2) a^2 cot(π/10) ≈ 7.694208843 * a^2
Khi xét về apothem r (tức là hình học trong đường tròn nội tiếp), diện tích được tính bằng công thức: A = 10 tan(π/10) r^2 ≈ 3.249196962 * r^2
Với bán kính ngoại tiếp R, diện tích được tính bằng công thức: A = 5 sin(π/5) R^2 ≈ 2.938926261 * R^2
Một công thức khác là A = 2.5 da, trong đó d là khoảng cách giữa các cạnh song song hoặc chiều cao khi đa giác đứng dựa trên một cạnh làm đáy, hoặc đường kính của đường tròn nội tiếp. Nhờ toán học đơn giản, ta có: d = 2a(cos(3π/10) + cos(π/10)), và nó có thể được viết dưới hình thức đại số là d = a sqrt(5 + 2√5).
Đa giác thập diện không lồi
Một tấm nền bằng các tam giác và có một đa giác ngoại tuyến của đa giác thập diện đều, ký hiệu Schäfli của nó là {10/3}.
Tỷ lệ hoàn hảo trong đa giác thập diện
Cả trong việc xây dựng với đường tròn ngoại tiếp và với độ dài cạnh đã cho, tỷ lệ hoàn hảo chia một đoạn thẳng bằng cách chia thành các phần bên ngoài các phần bên ngoài xác định phần tử xây dựng.
- Trong xây dựng với đường tròn ngoại tiếp, cung tròn quanh G với bán kính GE3 tạo ra đoạn AH, sự chia của nó tương ứng với tỷ lệ hoàn hảo. AM̅/MH̅ = AH̅/AM̅ = 1 + (√5) / 2 = Φ ≈ 1.618.
- Trong xây dựng với độ dài cạnh cho trước, cung tròn quanh D với bán kính DA tạo ra đoạn E10F, sự chia của nó tương ứng với tỷ lệ hoàn hảo. E1E10̅/E1F̅ = E10F̅/E1E10̅ = R/a = 1 + (√5) / 2 = Φ ≈ 1.618.
Đối xứng
Đa giác thập diện đều có đối xứng Dih10, bậc 20. Có 3 đối xứng nhóm dihedral: Dih5, Dih2 và Dih1, và 4 đối xứng nhóm tuần hoàn: Z10, Z5, Z2 và Z1. 8 đối xứng này có thể được nhìn thấy trong 10 đối xứng riêng biệt trên đa giác thập diện, một số lớn hơn vì các đường phản xạ có thể thông qua các đỉnh hoặc cạnh. John Conway đặt tên các đối xứng này theo một chữ cái và thứ tự nhóm.[7] Đối xứng đầy đủ của đa giác thập diện là r20 và không có đối xứng nào được đánh nhãn a1. Các đối xứng dihedral được chia thành hai nhóm tùy thuộc vào chúng có đi qua các đỉnh (d cho diagonal) hoặc cạnh (p cho perpendiculars), và i khi các đường phản xạ thông qua cả cạnh và đỉnh. Nhóm tuần hoàn nằm ở giữa được đánh nhãn là g cho các bước chuyển trung tâm của chúng. Mỗi đối xứng của các nhóm nhỏ cho phép một hoặc nhiều độ tự do cho các hình dạng không đều. Chỉ nhóm g10 không có bất kỳ độ tự do nào nhưng có thể được xem là cạnh hướng.
Phân tích
Một đa giác thập diện có thể được phân tích thành 10 hình thoi, ví dụ như hình dưới. Từ hình này, chúng ta có thể nhận thấy rằng mỗi một đa giác thập diện đều có thể được chia thành 80 mặt trong một mặt phẳng Petrie của 5-đa. Một phân tích được xây dựng từ 30 mặt của mặt phẳng tam giác thập diện. Số lượng giải pháp được định nghĩa trong OEIS: A006245 là 62 và có 2 hướng cho hình dạng đối xứng đầu tiên và 10 hướng cho 6 hình dạng khác.
Đa giác thập diện chính quy chia thành 10 hình thoi
Đa giác thập diện xoắn
Một đa giác xoắn chứa các cạnh zig-zag của một chóp ngũ giác, một chóp đa giác ngũ giác, và một chóp bắc qua chóp đa giác ngũ giác xoắn.
Hình ảnh của một đa giác thập diện xoắn được tạo ra bởi các cạnh zig-zag của một chóp ngũ giác, chóp đa giác ngũ giác xoắn và chóp bắc qua chóp đa giác ngũ giác xoắn. Một đa giác xoắn chính quy là có độ dài các cạnh bằng nhau. Trong không gian 3 chiều, nó sẽ là một đa giác xoắn zig-zag và có thể nhìn thấy trong các đỉnh và cạnh bên một chóp ngũ giác, chóp đa giác ngũ giác và chóp bắc qua chóp đa giác ngũ giác với cùng đối xứng D5d, [2+, 10], bậc 20.
Các đối tượng này cũng có thể được nhìn thấy trong bốn đa diện lồi với đối xứng icosahedron. Các đa giác trên chu vi của các hình chiếu này là đa giác xoắn chính quy.
Đa giác Petrie
Đa giác Petrie là đa giác Petrie cho nhiều đa diện có số chiều cao, được hiển thị trong các mặt phẳng chứa đường cong Coxeter:[9] Số lượng cạnh trong đa giác Petrie bằng số Coxeter, h, cho mỗi gia đình đối xứng. Đa giác thập diện xoắn chính quy là đa giác Petrie cho nhiều đa diện có số chiều cao, được hiển thị trong các mặt phẳng chứa đường cong Coxeter: A9, D6, B5, 9-simplex, 411, 131, 5-orthoplex, 5-cube.
Xem thêm
- Số đa giác thập diện và số đa giác trung tâm thập diện, số đa hình họa được mô phỏng trên đa giác thập diện.
- Decagram, một đa giác ngôi sao có cùng các đỉnh như đa giác thập diện chính quy.
Tham khảo
Weisstein, Eric W. "Decagon". MathWorld. Definition and properties of a decagon With interactive animation












