In the world of geometry, there is a polygon that possesses a unique charm and complexity - the dodecagon. With its twelve sides and twelve vertices, the dodecagon is a captivating shape that has intrigued mathematicians and artists alike. Let's dive into the enchanting world of the dodecagon and explore its properties and applications.
The Regular Dodecagon: A Perfect Harmony of Sides and Angles
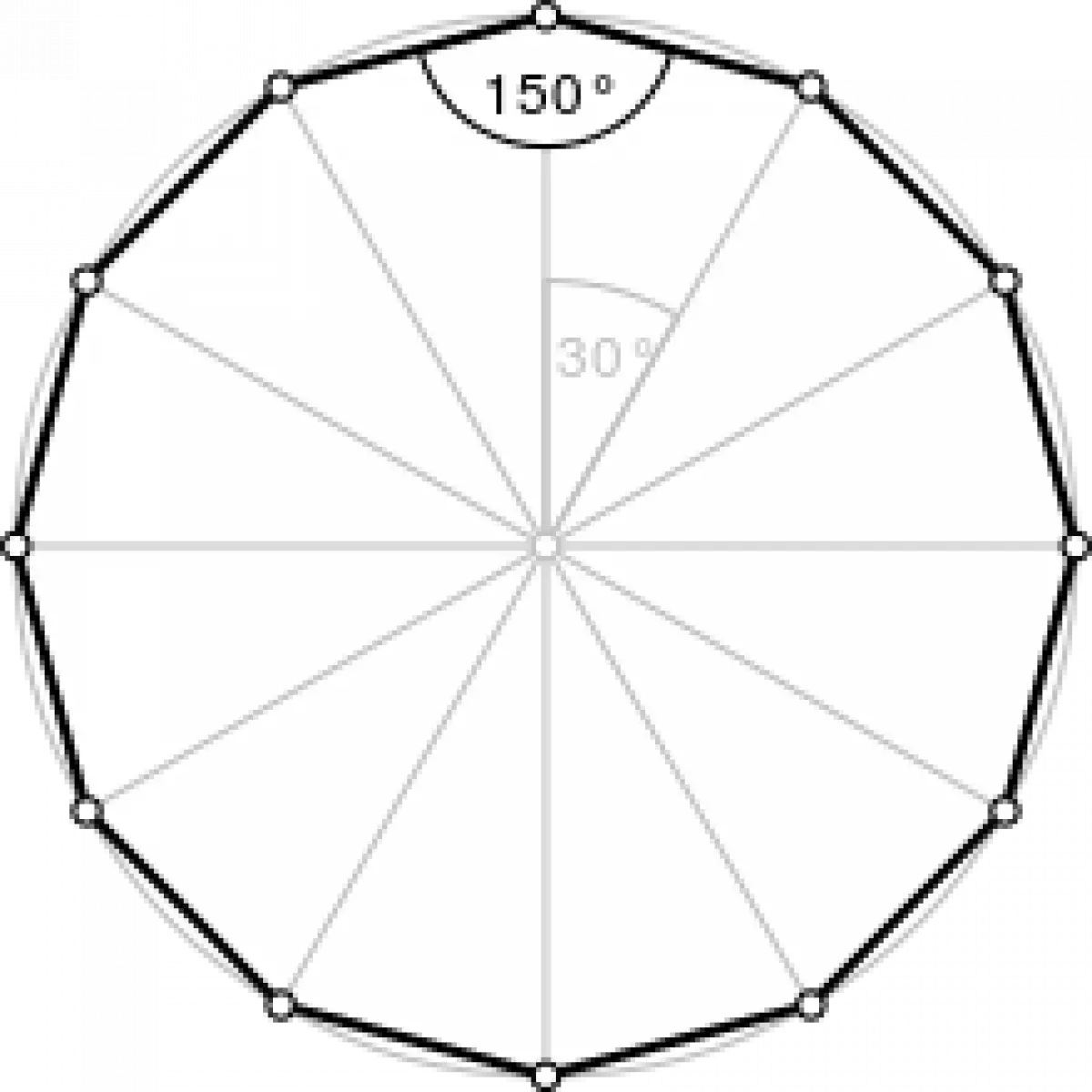
A regular dodecagon is a polygon with sides of equal length and internal angles of the same size. It boasts twelve lines of reflective symmetry and rotational symmetry of order 12. Represented by the Schläfli symbol {12}, the regular dodecagon can be constructed as a truncated hexagon (t{6}) or a twice-truncated triangle (tt{3}). Each internal angle of a regular dodecagon measures 150°, showcasing its remarkable symmetry.
Three squares of sides R can be cut and rearranged into a dodecagon of circumradius R, yielding a proof without words that its area is 3R^2.
Calculating the Area and Perimeter of a Dodecagon
Determining the area and perimeter of a regular dodecagon involves trigonometric calculations. The area of a regular dodecagon with side length a is given by:
A = 3 cot(π/12) a^2 ≃ 11.19615242 a^2
In terms of the apothem r (the distance from the center of the dodecagon to any side), the area is:
A = 12 tan(π/12) r^2 ≃ 3.2153903 r^2
Alternatively, the area can be expressed in terms of the circumradius R (the distance from the center of the dodecagon to any vertex):
A = 6 sin(π/6) R^2 = 3 R^2
The perimeter of a regular dodecagon can be calculated using its circumradius R:
p = 24 R tan(π/12) ≃ 6.21165708246 R
Or in terms of the apothem r:
p = 24 r tan(π/12) ≃ 6.43078061835 r
The Intricate Symmetry of Dodecagons
The regular dodecagon possesses Dih12 symmetry, with a total of 15 distinct subgroup dihedral and cyclic symmetries. Each subgroup symmetry allows for one or more degrees of freedom, resulting in irregular forms. Notably, the g12 subgroup exhibits rotational symmetry with no degrees of freedom, resembling directed edges.
The symmetries of a regular dodecagon shown with colored edges and vertices.
From Polyhedra to Patterns: Dodecagons in Practical Applications
The regular dodecagon finds its place not only in the realm of mathematics but also in various practical applications. It appears prominently in architectural designs, such as the Torre del Oro in Seville, Spain, and the Vera Cruz church in Segovia, Spain. The dodecagon is also a symbol used in many coins, including the British threepenny bit and the British one-pound coin.
The Vera Cruz church in Segovia, Spain, featuring a dodecagonal design.
Exploring the Vastness of Dodecagons
Beyond the regular dodecagon, there are fascinating variations to explore. Dodecagrams, star-shaped polygons, add a touch of elegance to the dodecagon family. Compounds of dodecagons, formed by combining multiple regular polygons, create intricate patterns that continue to captivate mathematicians and enthusiasts alike.
The world of dodecagons is a testament to the beauty and complexity of mathematics. From its geometric properties to its practical applications, the dodecagon continues to inspire and engage the curious minds of both professionals and enthusiasts.
So next time you encounter a dodecagon in architecture, art, or daily life, take a moment to appreciate its unique allure and the fascinating world of polygons it represents.
