Have you ever heard of a nonagon? It may sound like a complex term, but it's actually quite simple. In this article, we'll dive into the world of nonagons, exploring their definition, types, and even some examples. So, let's get started!
Unraveling the Mystery: What is a Nonagon?
A nonagon is a polygon with nine sides and nine interior angles. It's like a closed shape with straight line segments forming its sides. To give you a visual representation, take a look at the nonagon below.
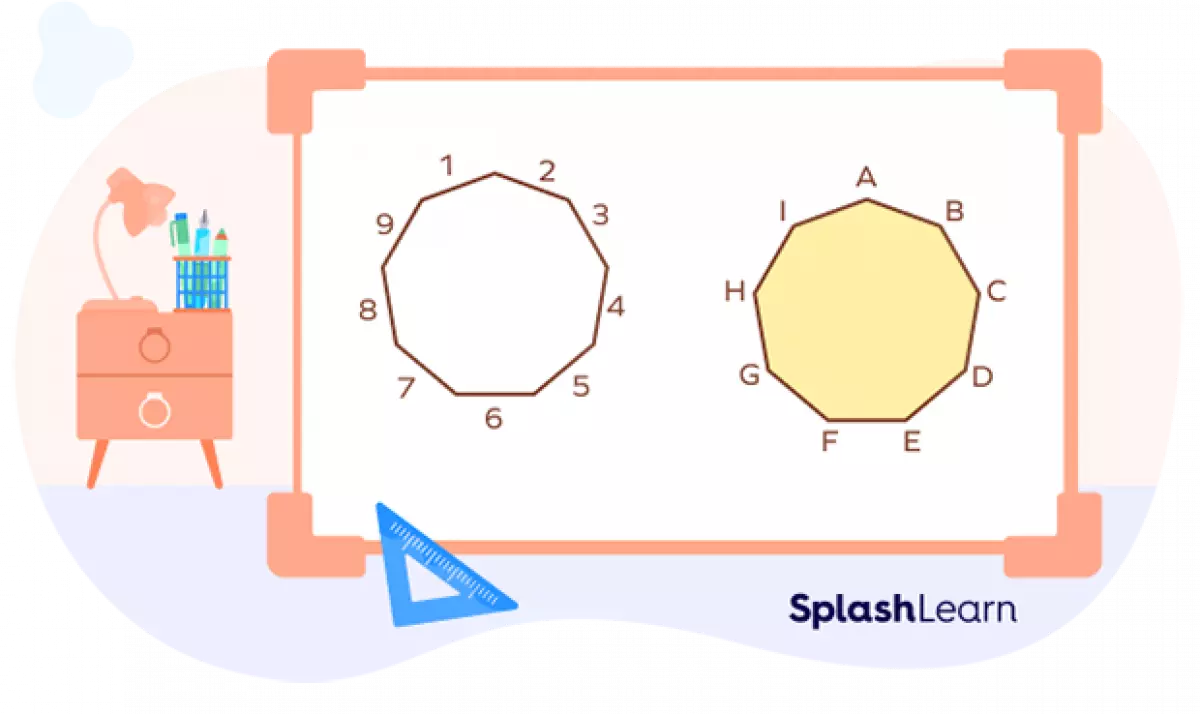Nonagon
Understanding the Types of Nonagons
Nonagons can be classified in different ways. Let's explore the two main types: regular and irregular nonagons.
Regular Nonagons and Irregular Nonagons
Regular Nonagons: These nonagons have equal sides and angles. Each side has the same length, and each angle measures the same. Here's an example to help you visualize a regular nonagon.
Regular nonagon
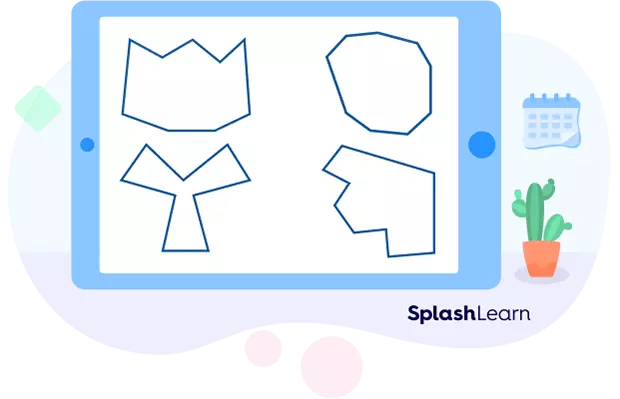
Irregular Nonagons: Irregular nonagons, on the other hand, have sides and angles that are not equal. Each side can have a different length, and each angle can measure differently. Take a look at the example below.
Irregular nonagons
Convex and Concave Nonagons
Another way to classify nonagons is based on their shape. Let's explore convex and concave nonagons.
Convex Nonagons: Convex nonagons have interior angles that are all less than 180°. In other words, they don't have any angles greater than 180°. All the diagonals of a convex nonagon lie inside the shape.
Concave Nonagons: Concave nonagons, on the other hand, have at least one interior angle greater than 180°. In concave nonagons, you'll find diagonals that extend outside the shape.
Here's a visual representation of convex and concave nonagons.
Convex nonagon
Concave nonagon
Simple and Complex Nonagons
Lastly, nonagons can be classified as simple or complex based on their intersections.
Simple Nonagons: Simple nonagons don't intersect themselves. The sides of a simple nonagon don't cross each other.
Simple nonagons
Complex Nonagons: Complex nonagons, on the other hand, have sides that intersect each other, creating additional interior spaces.
Complex nonagon
Exploring the Interior Angles, Perimeter, and Diagonals
Now that we understand the different types of nonagons, let's dive into some interesting facts and formulas associated with them.
Interior Angles of a Regular Nonagon
For a regular nonagon, each interior angle is calculated using the formula:
Interior angle of a regular polygon $= \frac{180n - 360}{n}$
For a nonagon with 9 sides, the interior angle is:
Interior angle of a regular nonagon $= \frac{(180 \times 9) - 360}{9} = 140°$
Sum of Interior Angles of a Nonagon
The sum of interior angles of any polygon can be calculated using the formula:
Sum of interior angles of a polygon $= (n - 2) \times 180°$
For a nonagon with 9 sides, the sum of interior angles is:
Sum of angles of a nonagon $= (9 - 2) \times 180° = 7 \times 180° = 1260°$
Number of Diagonals in a Nonagon
The number of diagonals in a polygon can be calculated using the formula:
Number of diagonals of a polygon $= \frac{n(n - 3)}{2}$
For a nonagon with 9 sides, the number of diagonals is:
Number of diagonals in a nonagon $= \frac{9 \times 6}{2} = 27$
Perimeter of a Regular Nonagon
The perimeter of a regular nonagon can be calculated by multiplying the length of one side by the number of sides. So, if each side of a regular nonagon is "a" units, the perimeter is:
Perimeter of a regular nonagon $= 9 \times a$ units
Conclusion
In this article, we explored the fascinating world of nonagons. We learned that a nonagon is a polygon with nine sides and nine interior angles. We also discussed different types of nonagons, including regular, irregular, convex, concave, simple, and complex nonagons. Additionally, we explored some interesting facts and formulas associated with nonagons. Now, armed with this knowledge, you can confidently tackle nonagon-related problems and explore the beauty of this unique shape.
