In the world of geometry, a regular hexagon stands out with its perfectly balanced six sides and six equal interior angles. In this article, we will explore the fascinating properties of this polygon, including its angles, perimeter, area, and even its relationship with equilateral triangles.
What Makes a Hexagon "Regular"?
A regular polygon is a convex shape where all sides and interior angles are equal. Specifically, a regular hexagon boasts six identical sides and six equal interior angles. This symmetry creates a visually pleasing shape that has captivated mathematicians and artists alike for centuries.
Behold the beauty of a regular hexagon.
Unveiling the Interior Angles
The sum of the interior angles in any polygon can be determined using the formula S = (n-2)•180°, where n represents the number of sides. For a hexagon, with n=6, the sum is calculated as (6-2)•180° = 4•180° = 720°. Since all interior angles in a regular hexagon are equal, each angle measures 720°/6 = 120°. From this fundamental fact, we can derive numerous other intriguing properties, such as the hexagon's association with six equilateral triangles.
A Stunning Composition of Equilateral Triangles
It's fascinating to discover that a regular hexagon can be dissected into six identical equilateral triangles. While some "proofs" may suggest complex techniques involving circles, we can formally prove this result in a more approachable manner.
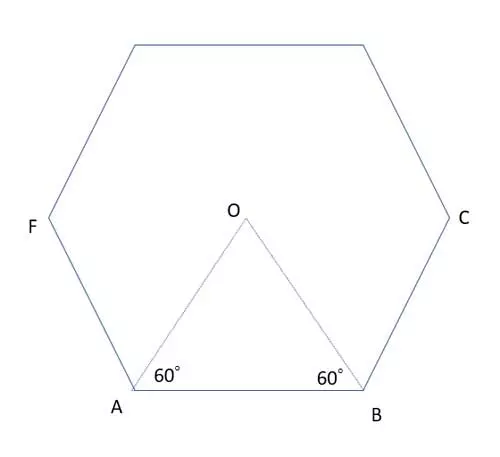
Let's draw the angle bisectors of two adjacent interior angles, intersecting at point O:
The angle bisectors form an equilateral triangle.
By observing the angles, we can see that triangle OAB is equilateral. The angle bisectors create two half angles measuring 60°: m∠OAB=m∠OBA=60°. Additionally, the sum of angles in a triangle dictates that ∠AOB is also a 60° angle, confirming that ΔOAB is an equilateral triangle.
Continuing the exploration, let's connect point O with vertex C and compare triangles ΔOAB and ΔOCB:
The triangles are congruent and equilateral.
We observe that OB=OB, AB=BC, and m∠ABO=m∠CBO=60°, as BO serves as the angle bisector. By the definition of congruent angles, we conclude that ∠ABO is congruent to ∠CBO. As a result, ΔOAB and ΔOCB are congruent triangles according to the Side-Angle-Side postulate. This process can be repeated for the remaining sides, connecting point O to vertices D, E, and F, leading us to the desired result: a regular hexagon composed of six identical equilateral triangles, all converging at its center, O.
Exploring Area and Perimeter
Knowing that a regular hexagon consists of six equilateral triangles allows us to easily calculate its area. The area of one equilateral triangle is given by the formula:
AreaΔequilateral = (s²√3)/4,
where s represents the length of a side. By applying this formula and multiplying it by the six triangles, we find that the area of the regular hexagon is:
Area⬡hex = 6•(s²√3)/4 = 3•√3•s²/2.
When it comes to the perimeter of any polygon, it simply means summing up the lengths of all its sides. In the case of a regular hexagon, since all sides are equal, the perimeter is:
P⬡hex = 6s.
The Role of the Radius
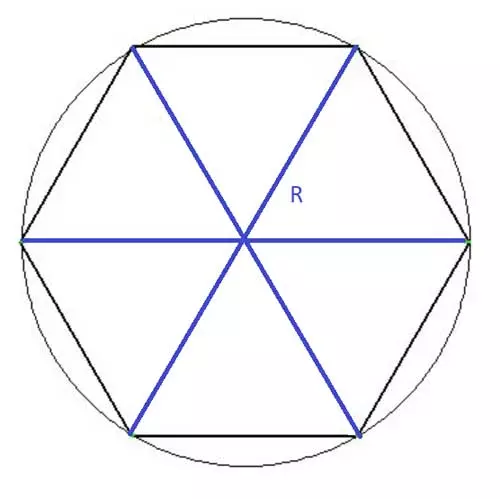
The radius of a regular polygon is the distance from its center to any of its vertices. Thanks to the symmetrical nature of the hexagon, this distance remains the same for all vertices. In the case of a regular hexagon, the center forms an equilateral triangle with the edges, making the radius (R) equal to the length of each side. This intriguing property also gives us the opportunity to inscribe a regular hexagon within a circle with radius R.
A regular hexagon neatly inscribed within a circle.
Understanding the intricacies of a regular hexagon allows us to appreciate its unique qualities and the captivating relationship it shares with equilateral triangles. From its angles to its area and perimeter, this polygon never fails to amaze both mathematicians and enthusiasts alike.
