In the realm of geometry, there exists a fascinating shape known as a nonagon. With its nine sides, this enigmatic polygon has captured the imagination of mathematicians and artists alike for centuries. Today, we will embark on a journey to discover the secrets of the nonagon and explore its captivating properties.
A Polygon with a Past
The nonagon, also known as an enneagon, derives its name from Latin and Greek origins. The term "nonagon" arose from the combination of the Latin word "nonus" meaning "ninth" and the Greek word "gonon" meaning "corner." On the other hand, "enneagon" directly translates to "nine angles" in Greek, making it a fitting alternative name for this intriguing shape.
Image: A visual representation of a nonagon
Unveiling the Regular Nonagon
At the heart of our exploration lies the regular nonagon, denoted by the Schläfli symbol {9}. This exceptional nonagon possesses several distinctive features. Its internal angles measure precisely 140°, granting it a unique symmetry. The area of a regular nonagon with a side length a can be determined using the formula:
A = (9/4) a^2 cot(π/9)
The radius r of the inscribed circle within a regular nonagon can be calculated as:
r = (a/2) * cot(π/9)
Furthermore, the radius R of the circumscribed circle can be found using the equation:
R = √((a/2)^2 + r^2) = r sec(π/9) = (a/2) csc(π/9)
Unconventional Constructions
While constructing a perfect regular nonagon with a compass and straightedge is impossible due to its mathematical properties, ancient approximations exist. These age-old methods come close to creating an accurate representation of this enigmatic shape, utilizing techniques such as neusis and angle trisection.
Image: Neusis construction of a nonagon based on angle trisection
A Symphony of Symmetry
The regular nonagon exhibits a fascinating array of symmetries, with its Dih9 symmetry boasting an order of 18. Within this overarching symmetry, subgroups such as Dih3, Dih1, Z9, Z3, and Z1 manifest themselves. These symmetries define the positioning and mirroring of the vertices and edges of the nonagon.
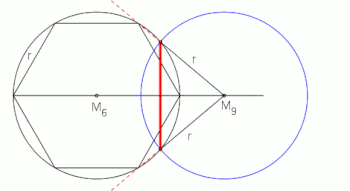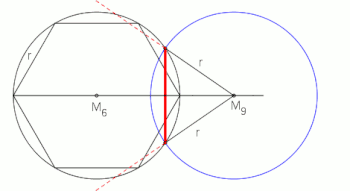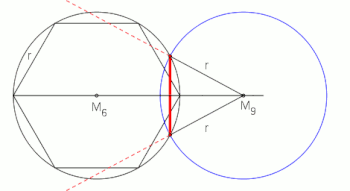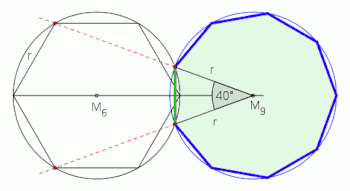Image: Symmetries of a regular nonagon
Where Art Meets Mathematics
The nonagon has found its place not only within the realms of geometry but also in various aspects of art and culture. From popular culture references in songs by They Might Be Giants and Slipknot to the album "Nonagon Infinity" by King Gizzard & the Lizard Wizard, this shape has truly permeated the creative sphere. Furthermore, Baháʼí Houses of Worship and architectural marvels like the U.S. Steel Tower proudly incorporate the nonagon into their designs.
Unraveling the Enigma
As we conclude our expedition into the world of the nonagon, we have unveiled its captivating properties, explored its mesmerizing symmetries, and discovered its role in art and architecture. The nonagon, with its enigmatic allure, continues to intrigue and inspire as a testament to the connection between mathematics and the world around us.
References:
- Properties of a Nonagon (with interactive animation)
