Introduction
Do you know what makes a nonagon so fascinating? Its unique structure and properties set it apart from other polygons. In this article, we will delve into the depths of the nonagon shape, uncovering its secrets and uncovering its hidden beauty.
What is a Nonagon Shape?
A nonagon, derived from the Latin words "nonus" and "gon," is a polygon with nine sides. This captivating geometrical figure can be regular or irregular, convex or concave, depending on the lengths of its sides and the measurements of its interior angles. Let's take a closer look at this mesmerizing shape.
Image: Nonagon - A polygon with 9 sides
As you can see in the image above, a nonagon consists of nine sides. Each side can be of equal length or different measures, adding to the allure of this shape.
Regular Nonagon vs. Irregular Nonagon
A regular nonagon is a true marvel. It possesses nine sides of equal length and nine interior angles of identical measure. On the contrary, an irregular nonagon showcases sides of various lengths and angles of different measures. Both variations of the nonagon shape have their own unique charm.
Properties of a Regular Nonagon
Let's explore the remarkable properties of a regular nonagon:
- All sides of a regular nonagon are of equal length, and all interior angles have the same measure.
- The sum of the interior angles of a regular nonagon is always 1260°, while the sum of the exterior angles is 360°.
- Each interior angle of a regular nonagon measures 140°.
Take a look at the figure below to visualize the difference between a regular and an irregular nonagon.
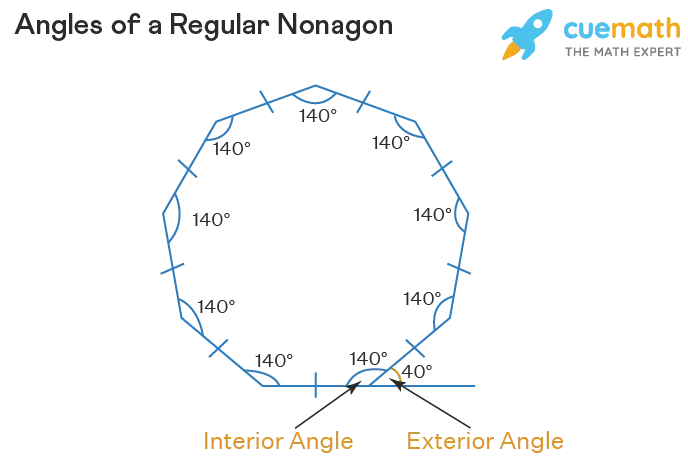Image: Regular Nonagon and Irregular Nonagon
Convex Nonagon and Concave Nonagon
The nonagon shape further amazes us with the concepts of convex and concave variations.
A convex nonagon possesses the following properties:
- All interior angles in a convex nonagon measure less than 180°.
- With interior angles smaller than 180°, convex nonagons seem to bulge outwards, catching our eye with their distinctive appearance.
On the other hand, a concave nonagon showcases the following properties:
- At least one interior angle in a concave nonagon is a reflex angle.
- The vertices of a concave nonagon can be oriented inwards, shaping its unique structure.
Witness the contrast between a convex and concave nonagon in the image below.
Image: Convex Nonagon and Concave Nonagon
Unveiling the Mystery of Nonagon Angles
Nonagons boast nine interior angles and nine corresponding exterior angles. Let's explore these angles and understand their significance in a regular nonagon.
Image: Angles of a Regular Nonagon
Nonagon Interior Angles
Each interior angle of a regular nonagon measures 140°. This calculation can be achieved using the formula for the interior angles of a regular polygon:
Interior angle of a regular polygon = (180n - 360) / n, where n represents the number of sides of the polygon. For a nonagon with n = 9, we substitute the value and find that each interior angle equals 140°.
The sum of the interior angles of any nonagon remains constant at 1260°, regardless of whether it is regular or irregular. This sum can be calculated using the formula:
Sum of interior angles of a polygon = (n - 2) × 180°, where n refers to the number of sides. Hence, for a nonagon with n = 9, we obtain:
Sum of interior angles of a polygon = (9 - 2) × 180° = 1260°.
Nonagon Exterior Angles
In a regular nonagon, each exterior angle measures 40°. By observing the aforementioned image, we can see that the exterior angle and interior angle form a linear pair, summing up to 180°. Therefore, the measure of each exterior angle in a regular nonagon is 180° - 140° = 40°. The total sum of the exterior angles in a nonagon is 360°.
Other Noteworthy Properties
To further distinguish the nonagon from other polygons, let's explore some of its noteworthy properties:
- A nonagon contains 9 sides, 9 interior angles, and 9 exterior angles.
- The sum of the interior angles in a nonagon is always 1260°.
- A nonagon possesses a total of 27 diagonals.
Delving into Nonagon Diagonals
Nonagons are adorned with 27 diagonals. These diagonals are formed by joining non-adjacent vertices of the shape. We can calculate the total number of diagonals in a nonagon using the formula:
Number of diagonals in a polygon = 1/2 × n × (n-3), where n stands for the number of sides in the polygon. With n = 9 in the case of a nonagon, when we substitute this value in the formula, we find:
Number of diagonals in a polygon: 1/2 × 9 × (9-3) = 27. Therefore, a nonagon boasts exactly 27 diagonals.
Determining the Perimeter of a Nonagon
The perimeter of a polygon is the total length of its boundary. To find the perimeter of a nonagon, we need to determine the lengths of all nine sides and sum them accordingly. In the case of a regular nonagon, where all sides have equal lengths, we can multiply the length of one side by 9 to calculate the perimeter. These formulas can be expressed as follows:
- Perimeter of a nonagon = Sum of all its sides
- Perimeter of a regular nonagon = 9a (where a refers to the length of one side of the nonagon)
Conclusion
The nonagon shape captivates us with its nine sides, nine interior angles, and nine exterior angles. Its distinct properties, such as the sum of interior angles always equating to 1260°, 27 mesmerizing diagonals, and the unique characteristics of convex and concave variations, make the nonagon a true marvel in the world of polygons. Explore the realm of the nonagon and appreciate its beauty, for it is a shape that leaves an indelible mark on geometry.
☛ Related Articles:
- Types of Polygon
- Pentagon
- Hexagon
- Heptagon
- Octagon
- Decagon
- Dodecagon
- Dodecahedron
