Are you ready to explore the captivating world of polygon angles? In this article, we will unravel the mysteries behind the interior and exterior angles of polygons. So, buckle up and let's dive in!
Understanding Interior Angles
The angles that reside inside a polygon are known as its interior angles. To get a visual understanding, take a look at this 5-sided irregular polygon:
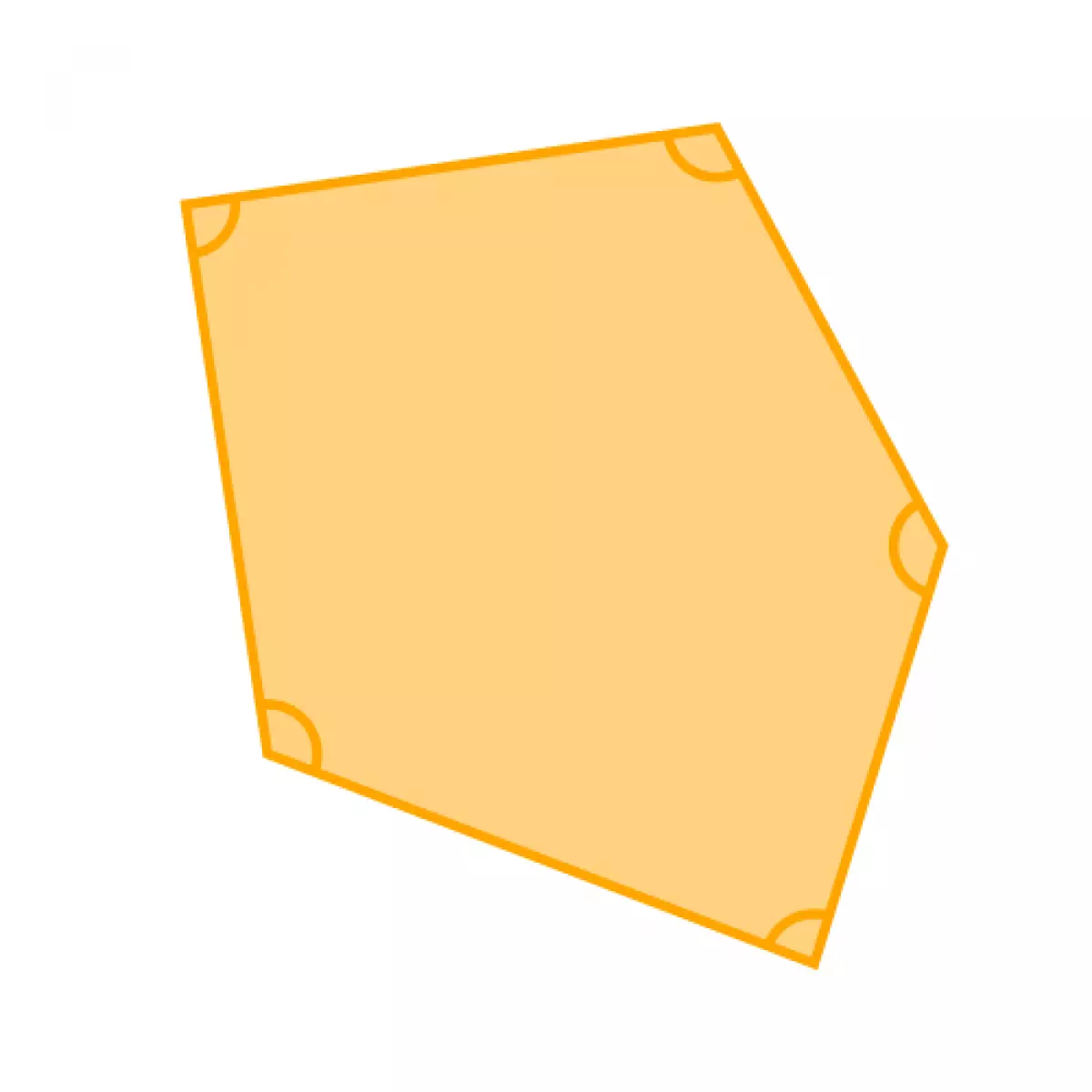Figure 1: An irregular polygon showcasing its interior angles
Embarking on an Exterior Adventure
When we extend one side of a polygon, the angle formed between the extended side and the adjacent side is called an exterior angle. We can do this for each side of the shape. Take a look:
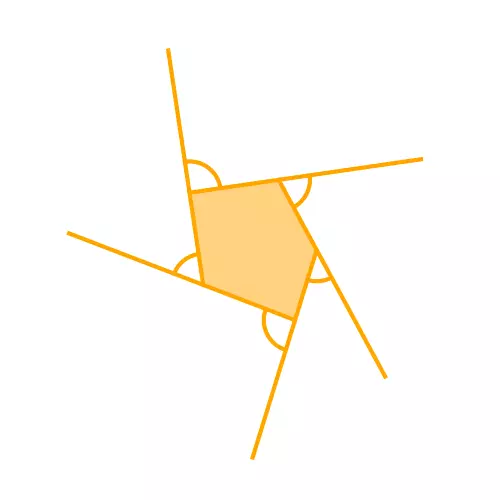Figure 2: Exterior angles of a polygon
Unveiling the Secret of the Sum
Have you ever wondered why the sum of the exterior angles in a polygon always adds up to 360°, regardless of the number of sides it possesses? Let's dive into an intriguing explanation.
Imagine an ant crawling along the outside of the polygon in a clockwise direction. Every time it reaches a corner, the ant turns to its right, aligning itself with the next side. Each turn corresponds to the exterior angle of that corner. When the ant completes its journey, it will have turned through a total of 360°, facing the same direction as it started. This remarkable phenomenon reveals that the sum of the exterior angles in any polygon is always 360°.
To emphasize this concept, let's visualize it with decreasingly sized polygons:
Figure 3: Same-shaped polygons with varying sizes
Even though the shape becomes smaller, the sum of the exterior angles remains constant. This reinforces the idea that the sum of exterior angles in a polygon is always 360°.
For regular polygons, where each exterior angle is the same, an exterior angle of an n-sided polygon is equal to 360°/n. Let's examine a regular pentagon as an example:
Figure 4: The sum of exterior angles in a regular pentagon
Delving into Interior Angles
Determining the sum of interior angles is not as straightforward as the sum of exterior angles. However, we can apply a simple formula that revolves around the number of sides, n:
Sum of Interior Angles = (n - 2) x 180°
To comprehend this formula, let's divide a polygon into triangles:
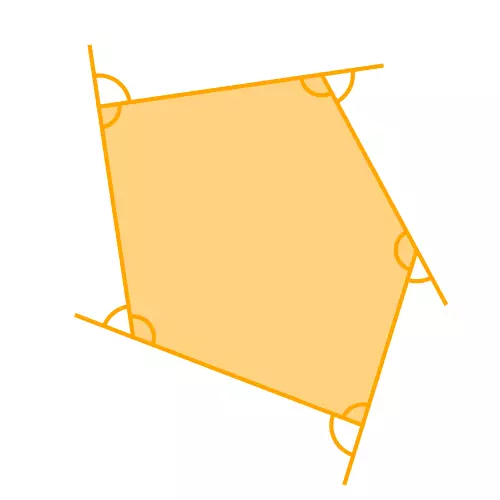Figure 5: Dividing a polygon into triangles
In this example, we have a 5-sided polygon (pentagon), which can be divided into 3 triangles. As we know, the interior angles of a triangle add up to 180°. Therefore, the sum of the interior angles in a 5-sided polygon is 3 x 180°, aligning perfectly with our formula.
The formula (n - 2) x 180° applies to all polygons. A 6-sided shape can be divided into 4 triangles, a 7-sided shape into 5 triangles, and so on.
For regular polygons, where each interior angle is the same, an interior angle of an n-sided polygon is:
Interior Angle = [(n - 2) x 180°] / n
Let's witness this concept in action using a regular pentagon:
Figure 6: The sum of interior angles in a regular pentagon
An Alternative Perspective
There is an alternative way to view interior and exterior angles, which ultimately leads to the same results. Let's explore this unique outlook.
Consider the same polygon, but this time, the interior and exterior angles at each corner form a straight line. In other words, they add up to 180°.
This means that for an n-sided shape, the total of all the interior and exterior angles is:
Sum of Interior and Exterior Angles = n x 180°
Since the total of the exterior angles is 360°, the total of interior angles can be calculated as:
Sum of Interior Angles = (n x 180°) - 360°
Simplifying this equation, we arrive at the familiar formula:
Sum of Interior Angles = (n - 2) x 180°
In Conclusion
Polygon angles possess a captivating allure, ranging from the mystical sum of exterior angles to the intriguing sum of interior angles. By understanding these concepts, you unlock the secrets to deciphering the characteristics of any polygon. Embrace the beauty of geometry as you explore the intricacies of shapes.
Sources
- Regular polygons
- Triangles
- Quadrilaterals
- Quadrilateral family tree
- Pentagons - polygons with 5 sides
- Hexagons - polygons with 6 sides
- Heptagons - polygons with 7 sides
- Octagons - polygons with 8 sides
- Nonagons - polygons with 9 sides
- Decagons - polygons with 10 sides
- Hendecagons - polygons with 11 sides
- Dodecagons - polygons with 12 sides
- N-gons - polygons with any number of sides
- Other types of polygon
- Star polygons
