Have you ever wondered about shapes with intriguing angles? Well, let's dive into the world of heptagons! A heptagon is a two-dimensional figure with seven sides and seven angles. In simpler terms, it's a polygon made up of straight lines without any curves.
Unveiling the Mystery
The word "heptagon" is derived from two words - "hepta" meaning seven in Greek, and "gonia" meaning angle. Fascinating, isn't it? In Latin, it's known as a septagon, where "septa" indicates seven and "gon" implies angles.
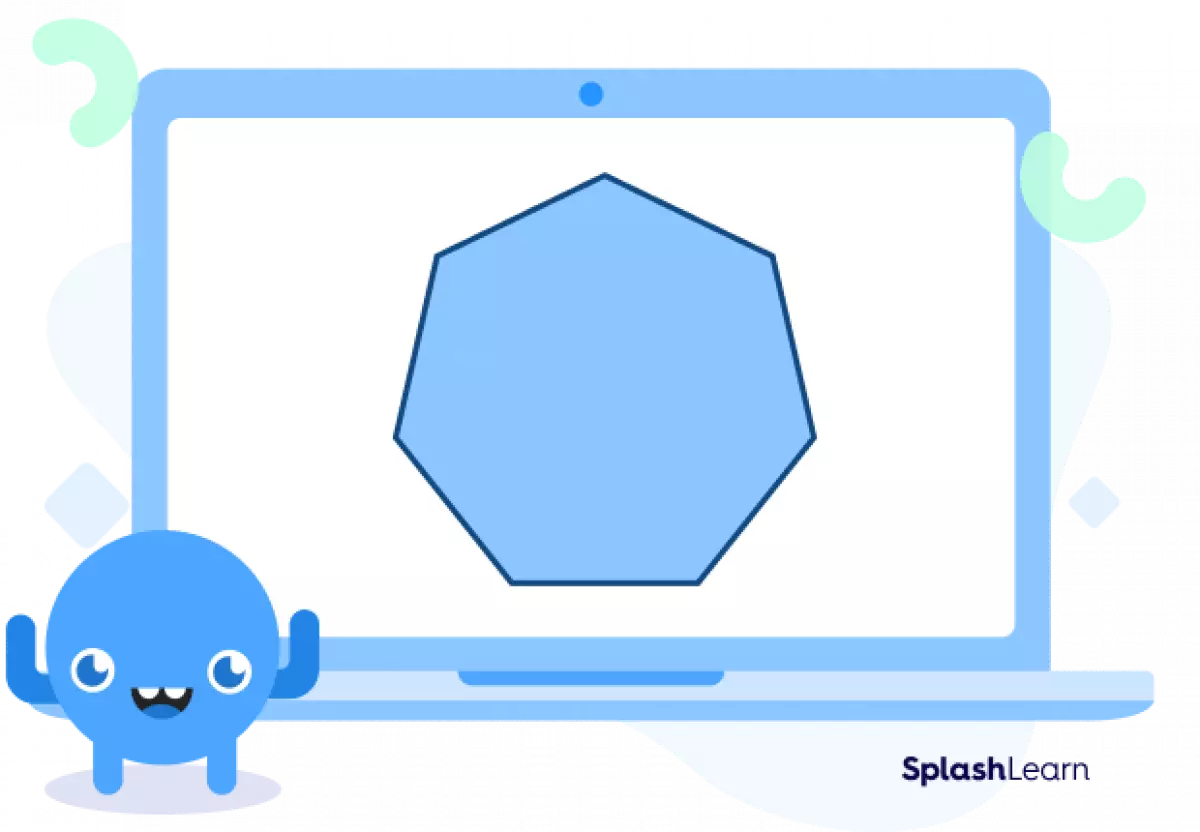 Caption: A mesmerizing regular heptagon
Caption: A mesmerizing regular heptagon
Unraveling the Properties
Let's explore some interesting properties of heptagons:
- A heptagon consists of seven sides, angles, and vertices.
- The sum of interior angles in a heptagon amounts to 900°.

- Heptagons have 14 diagonals.
Deconstructing Types
There are two types of heptagons based on their shapes. Let's take a closer look:
- Regular Heptagon: It exhibits equal sides and angles. Each angle measures approximately 128.57°, and the sides have the same length. No parallel sides are present.
Properties of a Regular Heptagon:
- The sum of its exterior angles is 360°.
- The measure of each interior angle is approximately 128.57°.
- The central angle of a regular heptagon measures about 51.43°.
- A regular heptagon has 14 diagonals.
 Caption: Angle measures in a regular heptagon
Caption: Angle measures in a regular heptagon
 Caption: Diagonals in a regular heptagon
Caption: Diagonals in a regular heptagon
- Irregular Heptagon: Unlike its regular counterpart, this heptagon showcases sides and angles of varying lengths and degrees. It can possess two or more pairs of parallel sides.
For instance, consider the images below of a coin and an arrow.
 Caption: Coin - a regular heptagon. Arrow - an irregular heptagon.
Caption: Coin - a regular heptagon. Arrow - an irregular heptagon.
So, the next time you encounter objects such as these, don't be perplexed! They are indeed heptagons, just like the images below!
Convex or Concave?
Heptagons can be classified as either convex or concave. Let's explore:
- Concave heptagon: It features at least one angle pointing inward, while all other angles point outward. Additionally, one or more interior angles of a concave heptagon exceed 180°.
- Convex heptagon: All interior angles are less than 180°, appearing to point outward. A regular heptagon always falls under this category.

Unveiling the Perimeter
The perimeter of a shape is the total length of its boundary. For a polygon like a heptagon, the perimeter is calculated by summing the lengths of all its sides.
Let's consider a regular heptagon with each side measuring "a" unit. In this case, the perimeter is given by the formula:
Perimeter = 7a units

Real-life Encounters
Heptagons may go unnoticed in our daily lives, but they exist in various forms. Here are a few examples:
- Cacti: Certain cacti, when viewed from above, form heptagons.
- Greenhouses: The front view of a greenhouse often reveals its heptagonal shape.

Solving Puzzles
Let's solve some practice problems to solidify our understanding:
1. Find the perimeter of a regular heptagon with a side length of 15 cm. Solution: Given the side length "a" as 15 cm, the perimeter is calculated using the formula:
Perimeter = 7a = 7 * 15 = 105 cm.
2. Determine the perimeter of an irregular heptagon with sides measuring 7 cm, 8 cm, 9 cm, 10 cm, 11 cm, 12 cm, and 13 cm. Solution: The perimeter is calculated by adding the lengths of all the sides:
Perimeter = 7 cm + 8 cm + 9 cm + 10 cm + 11 cm + 12 cm + 13 cm = 70 cm.
3. What is the side length of a regular heptagon with a perimeter of 224 cm? Solution: Given that the perimeter is 224 cm, we can find the side length "a" using the formula:
Perimeter = 7a. 224 = 7a. a = 224/7. a = 32 cm.
Exploring Further
Heptagons have piqued your interest! Now, take on these practice problems to deepen your knowledge.
Frequently Asked Questions
Still curious? Here are some commonly asked questions about heptagons.












