Have you ever wondered about the mysterious angles that exist outside a polygon? Well, those are known as exterior angles, and they have some intriguing properties. In this article, we'll explore the concept of exterior angles in polygons and uncover their secrets.
What are Exterior Angles?
An exterior angle of a polygon is the angle formed between any side of the polygon and a line extended from the next side. To put it simply, it's the angle that lies outside the polygon. Every polygon, whether regular or irregular, has both interior and exterior angles. But our focus today is on those elusive exterior angles.
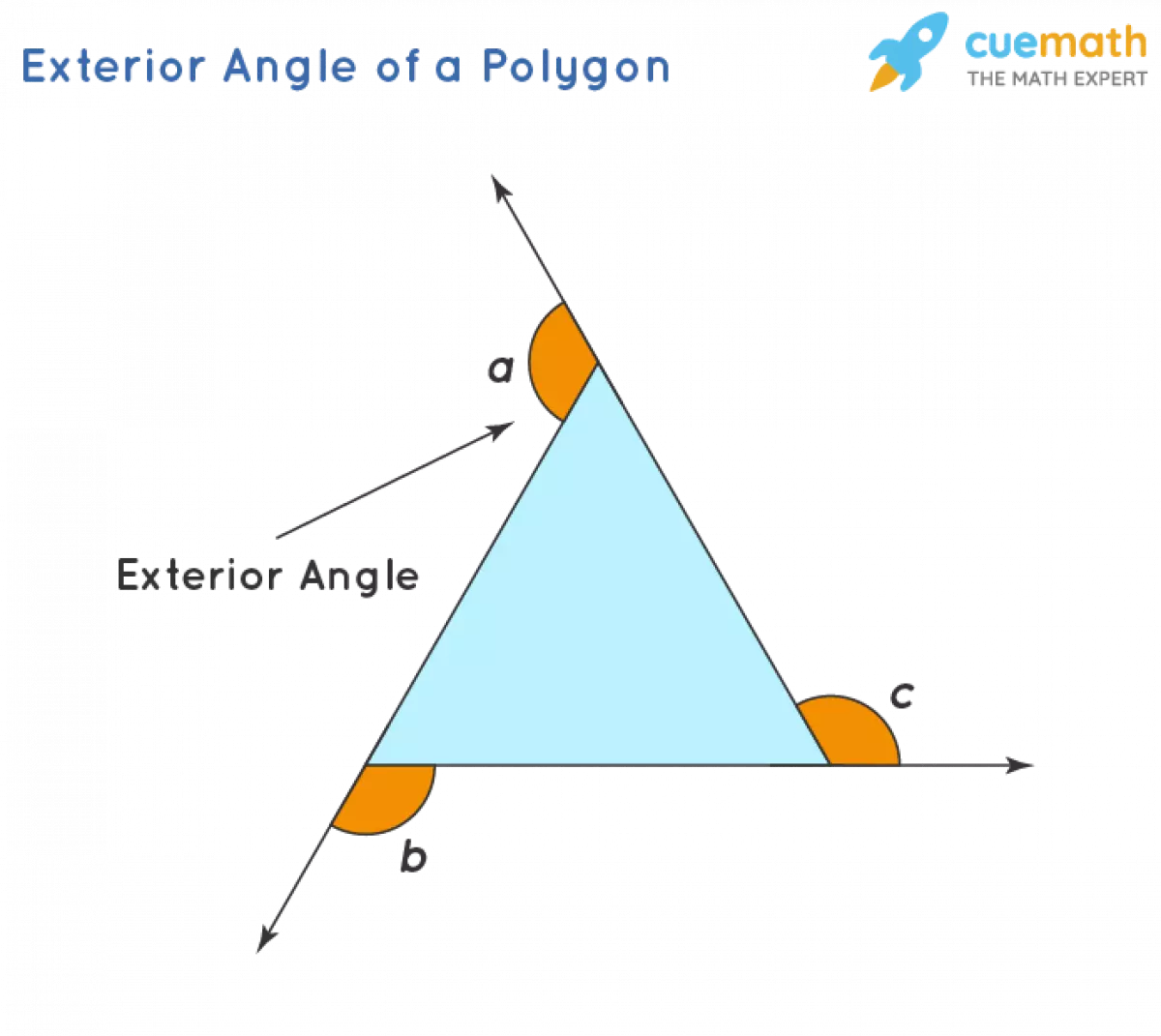Exterior Angle of a Polygon
The Fascinating Sum of Exterior Angles
One intriguing fact about exterior angles is that the sum of all the exterior angles of any polygon is always equal to 360°. It's like taking a full circle tour around the polygon! This holds true for both regular polygons, where all sides and angles are of equal measure, and irregular polygons, which have sides and angles of different measures.
Let's break it down further by looking at some examples.
Exterior Angles of a Regular Polygon
Consider a regular hexagon with six sides and six angles. If we assume that each exterior angle of the hexagon is equal to 'k', we can see that the hexagon creates a complete circle when we travel along its boundary. Since a circle is 360°, the sum of the exterior angles of the hexagon must also be 360°. Therefore, 6k = 360°, and each exterior angle measures 60°.
Exterior Angles of a Regular Polygon
Exterior Angles of an Irregular Polygon
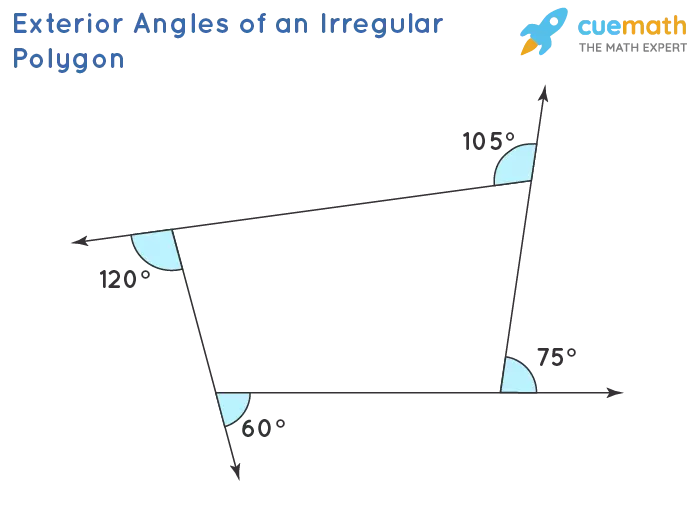
In an irregular polygon, where sides and angles have different measures, we can still observe that the sum of the exterior angles is 360°. Take a look at the figure below, depicting a quadrilateral with four unequal sides and angles. The exterior angles in this irregular polygon add up to 360° as well.
Exterior Angles of an Irregular Polygon
The Formula for Exterior Angles
Now that we understand the sum of the exterior angles, what about the measure of each individual angle? For both regular and irregular polygons, the measure of an exterior angle can be calculated using a simple formula. The exterior angle of a polygon is equal to 360° divided by the number of sides of the polygon.
An exterior angle of a polygon = 360° / Number of sides of the polygon.
The Theorem of Exterior Angles
Here's an interesting theorem about the sum of exterior angles in convex polygons: If a polygon is convex, meaning it has no indentations or concave parts, then the sum of its exterior angles, considering one at each vertex, will be equal to 360°.
The proof involves considering a polygon with 'n' sides. By applying the properties of linear pairs and interior angles, we can derive that the sum of exterior angles is indeed 360°.
Conclusion
Exterior angles add a fascinating dimension to the world of polygons. Whether in regular or irregular polygons, the sum of these angles always adds up to 360°, creating a full circle experience. So next time you encounter a polygon, take a moment to appreciate its exterior angles and the hidden wonders they hold.
Topics Related to Exterior Angles of a Polygon
- Definition of a Polygon
- Polygon Shape
- Regular Polygon
- Area of a Regular Polygon
- Interior Angles of a Polygon Calculator
- Exterior Angle Theorem
