Introduction
Are you familiar with the regular octagon? This polygon, with its eight sides and eight vertices, has a fascinating structure and various properties that make it intriguing to explore. In this article, we will delve into the theoretical background, properties, and formulas associated with the regular octagon. Whether you're a geometry enthusiast or simply curious about geometric shapes, this guide will provide you with valuable insights.
Definitions
Let's start by understanding the basic definitions of an octagon. An octagon can be either convex or concave. A convex octagon has no interior angles greater than 180°, while a concave octagon has at least one interior angle greater than 180°. A regular octagon, on the other hand, has equal sides and equal interior angles.
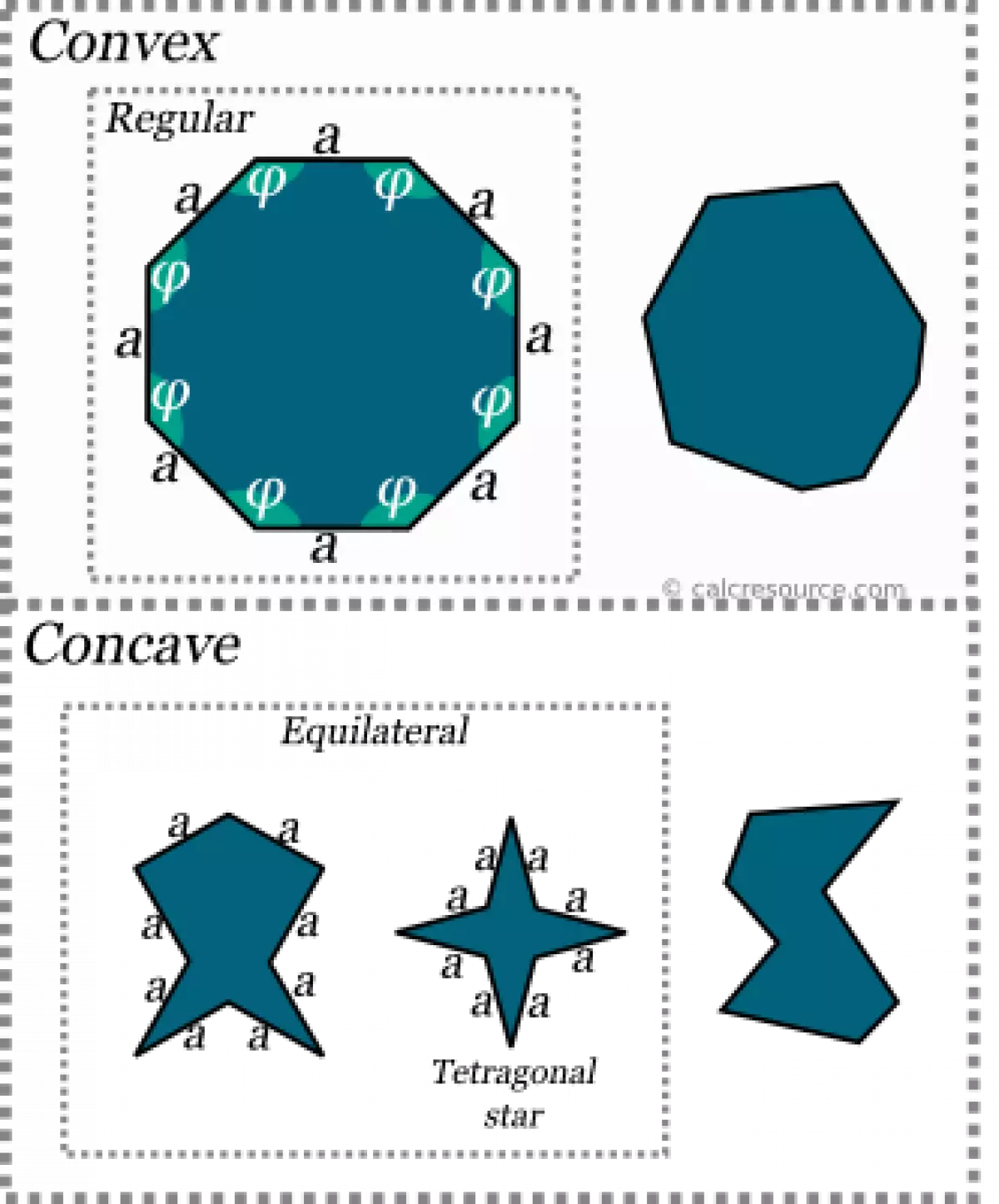Fig. 1: A regular octagon with equal sides and equal interior angles.
The sum of the internal angles of any octagon, whether convex or concave, is always 1080°. This can be understood by dividing the octagon into six triangles, resulting in a total of 180° per triangle.
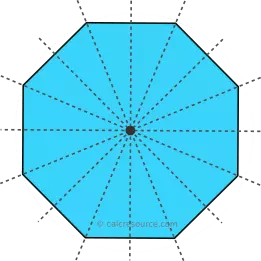Fig. 2: The diagonals of an octagon separate its interior into six triangles.
Properties of Regular Octagons
Regular octagons possess several interesting properties that make them unique.
Symmetry
A regular octagon features eight axes of symmetry. Half of these axes pass through diagonally opposite vertices, while the remaining axes pass through the midpoints of opposite edges.
Fig. 3: Axes of symmetry of a regular octagon.
Interior Angle and Central Angle
A regular octagon has eight equal interior angles. Each interior angle measures 135°. The central angle, which is the angle between two successive diagonals of the octagon, measures 45°. The interior and central angles are supplementary, with a sum of 180°.
Circumcircle and Incircle
Similar to other regular polygons, a regular octagon can be inscribed in a circle that passes through all eight vertices. This circle is known as the circumcircle. The diagonals of the octagon serve as diameters of the circumcircle. Additionally, a circle can be drawn that touches the midpoints of the octagon's edges, known as the inscribed circle. The circumradius is the radius of the circumcircle, while the inradius is the radius of the inscribed circle.
Fig. 4: Circumscribed and inscribed circles of a regular octagon.
Area and Perimeter
The total area of a regular octagon can be divided into eight identical isosceles triangles. Each triangle's area is equal to half the product of the octagon's edge length and the inradius. Therefore, the total area of the octagon is given by the formula A = (2a^2) / tan(22.5°), where a represents the edge length.
The perimeter of a regular octagon is simply eight times the length of one of its edges.
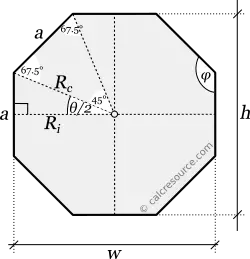
Bounding Box
The bounding box of a regular octagon is the smallest rectangle that completely encloses the shape. In the case of a regular octagon, the bounding box is a square due to its symmetry. The height and width of this square are equal to twice the inradius of the octagon.
Fig. 5: Bounding box of a regular octagon.
How to Draw a Regular Octagon
Drawing a regular octagon can be easily accomplished using a ruler and a compass. Follow these steps:
- Draw a line slightly longer than the desired diameter of the circumcircle.
- Mark two points on the line: one as the center of the polygon (point O), and the other as a point on the circumcircle (point A). Draw a circle with the center at point O and a radius equal to the circumradius (Rc).
- Construct a circular arc with its center at point A and a radius slightly larger than Rc.
- Repeat step 3, but with the center at point B (the intersection of the circumcircle and the line) and the same radius.
- Draw a line passing through the intersections of the arcs from step 4, as well as the center point O. Mark the two new intersection points as C and D, respectively.
- Using the same radius as in step 4, draw a circular arc with point C as the center. Mark the intersection point with the circumcircle.
- Repeat step 6, but with point D as the center. Mark another intersection point with the circumcircle.
- Draw a line passing through the intersection point marked in step 6 and the center point O. Mark the two new intersection points as E and F, respectively.
- Draw another line passing through the intersection point marked in step 7 and the center point O. Mark the two new intersection points as G and H, respectively.
- Connect the eight intersection points (A, B, C, D, E, F, G, and H) with straight lines to complete the regular octagon.
Fig. 6: Drawing a regular octagon using a ruler and a compass. Note the change in compass opening between steps 2 and 3.
Examples
To provide a quick reference, here are the main formulas associated with the regular octagon:
| Property | Formula |
|---|---|
| Circumradius (Rc) | 1.307a |
| Inradius (Ri) | 1.207a |
| Height (h) | 2.414a |
| Width (w) | 2.414a |
| Area (A) | 4.828a^2 |
| Perimeter (P) | 8a |
Conclusion
The regular octagon is a captivating geometric shape with symmetrical properties and intriguing formulas. By understanding its definitions, properties, and drawing techniques, you can appreciate its beauty and apply its principles to various areas of design, architecture, and mathematics. So, why not explore the fascinating world of regular octagons and expand your geometric knowledge?
