Understanding Angles in a Pentagon

A pentagon is a fascinating shape with five sides and five angles. While it may seem simple, there is more to angles in a pentagon than meets the eye. In this article, we will explore the different types of pentagons and delve into the sum and characteristics of the angles within them.

Types of Pentagons

Before we dive into the intricacies of angles, let's familiarize ourselves with the various types of pentagons. Pentagons can be classified based on their sides, angles, and vertices. Here are the types of pentagons you should know:

• Regular Pentagon: All sides and interior angles are equal.
• Irregular Pentagon: Sides and angles are not equal.
• Convex Pentagon: Vertices point outwards, and interior angles are less than 180°.
• Concave Pentagon: One interior angle is more than 180°, and vertices point inwards.

Take a look at the image below to visualize these types of pentagons.

Understanding the Pentagon

The word "pentagon" is derived from the Greek words "penta," meaning five, and "gon," meaning angle. It is a two-dimensional polygon with five sides and five angles. You can find real-life examples of pentagons in various objects, such as the black sections on soccer balls, school crossing signs, and even the Pentagon building in the USA.

Interior Angles

In a regular pentagon, an interior angle is the angle inside the shape and formed by two joined sides. The total number of interior angles in any polygon is equal to the number of sides. For a pentagon, there are five interior angles.

To calculate the measure of each interior angle in a regular pentagon, you can use the following formula:

Each interior angle = [(n - 2) × 180°] / n

In the case of a pentagon, where n = 5, substituting the values into the formula gives us:

Each interior angle = [(5 - 2) × 180°] / 5 = (3 × 180°) / 5 = 108°

Take a look at the image below to visualize the interior angles of a regular pentagon.

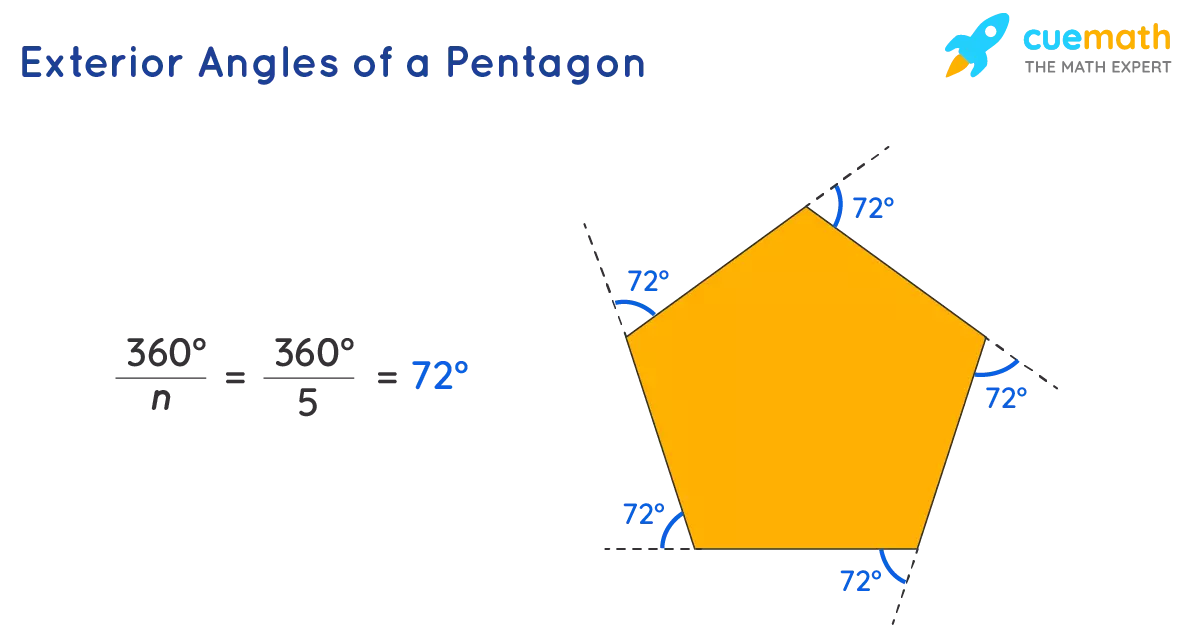
Exterior Angles

When a side of a pentagon is extended, the angle formed outside the pentagon with its side is called the exterior angle. In a regular pentagon, each exterior angle is equal to 72°. The sum of the exterior angles of any regular pentagon is 360°.

The formula for calculating the exterior angle of a regular polygon is:

Exterior angle of a regular polygon = 360° ÷ n

Where n represents the total number of sides in a pentagon.

Take a look at the image below to visualize the exterior angles of a pentagon.

Central Angles

The center of a pentagon is the point equidistant from each vertex or corner. When this center point is joined to all the vertices, it forms five central angles at the center. There are two methods to calculate the measure of a central angle in a pentagon.

Method 1:

1. Mark the center of the pentagon and join it to the vertices, forming five triangles.
2. As the center is equidistant from all the vertices, and all sides of a regular pentagon are equal, these triangles will be isosceles and congruent to each other. Therefore, the angles at the center will be equal.
3. Since each interior angle of a pentagon measures 108°, bisecting them will result in angles measuring (108°/2) = 54°.
4. Apply the angle sum property of a triangle to find the central angle: Central angle of a regular pentagon = 180° - (2 × 54°) = 72°

Method 2:

1. Mark the center of the pentagon and draw congruent triangles as shown in the previous method.
2. Since all five angles at the center are equal, each angle measures 360° ÷ 5 = 72°.

Take a look at the image below to visualize the central angles in a pentagon.

Sum of Interior and Exterior Angles in a Pentagon

The sum of the angles in any polygon depends on the number of sides it has. In the case of a pentagon, which has 5 sides, we can calculate the sum of its interior and exterior angles.

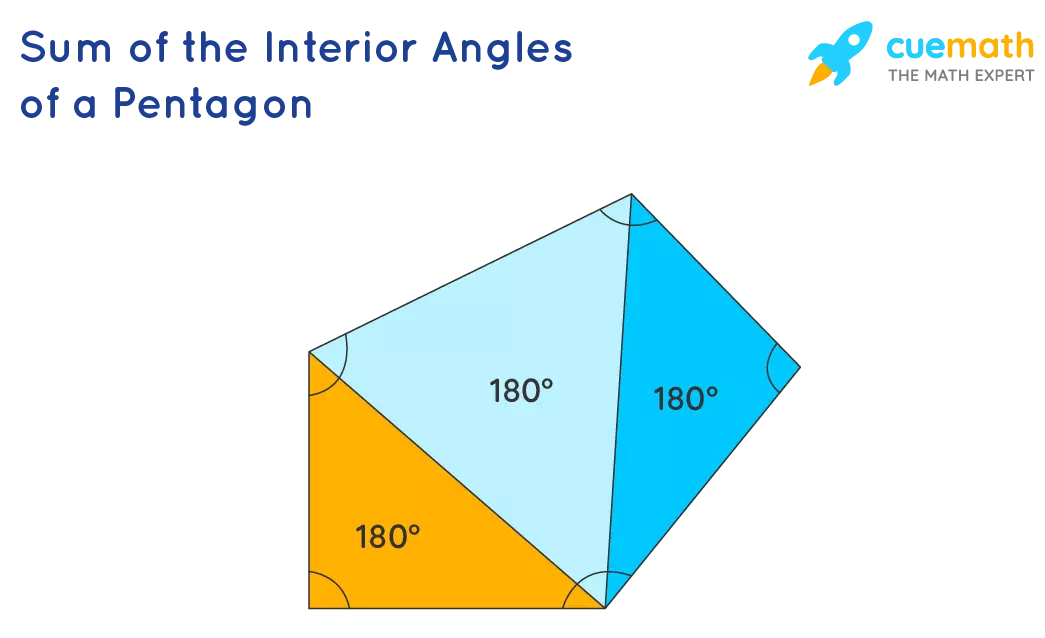
Sum of Interior Angles in a Pentagon

To find the sum of the interior angles of a pentagon, we divide it into triangles. In a pentagon, three triangles can be formed. Each triangle's angles sum up to 180°. So, to find the interior angles of the pentagon, we multiply the sum of the triangle angles by the total number of triangles:

180° × 3 = 540°

Take a look at the image below to visualize the sum of the interior angles of a pentagon.

Alternatively, you can use the formula:

Sum of angles = (n - 2) × 180°

Where 'n' represents the number of sides of the polygon. Substituting 'n' as 5 for a pentagon, we get:

(5 - 2) × 180° = 540°

Sum of Exterior Angles in a Pentagon

The sum of the exterior angles of any polygon is equal to 360°. Let's prove this in the case of a pentagon:

• The sum of the interior angles of a regular pentagon with 'n' sides = 180(n - 2).
• Each interior angle is: 180 (n - 2) / n.
• Each exterior angle is supplementary to the interior angle, so each exterior angle will be: [180n - 180n + 360] / n = 360/n.
• The sum of the exterior angles will be: n × (360/n) = 360°.

Important Notes

Here are a few key points to remember about angles in a pentagon:

• A pentagon is a two-dimensional polygon with five angles and five sides.
• The sum of all the interior angles of any regular pentagon equals 540°, and the sum of all the exterior angles of any regular pentagon equals 360°.
• Each exterior angle of a regular pentagon is equal to 72°, and each interior angle of a regular pentagon is equal to 108°.

Now that you have a better understanding of angles in a pentagon, you can appreciate the complexity and beauty of this geometric shape.