Let's chat about "entropy." Now, before you picture messy rooms and physics textbooks, hold on! In the world of information theory, entropy takes on a slightly different (but equally cool) meaning.
In a nutshell, entropy is all about measuring surprise. Imagine you're flipping a coin. If it lands on heads, you're probably not that surprised. It's a 50/50 chance, right? But what if someone told you they could predict the coin toss every single time? That would be surprising! Why? Because they've eliminated the uncertainty – the entropy – of the situation.
This idea, pioneered by the brilliant Claude Shannon, is at the heart of how we send information efficiently. Think about compressing files on your computer. A jumbled mess of random letters has high entropy – it's hard to predict what comes next. But a text document, with its patterns and predictable grammar, has lower entropy. We can exploit that predictability to represent the same information using fewer bits and bytes.
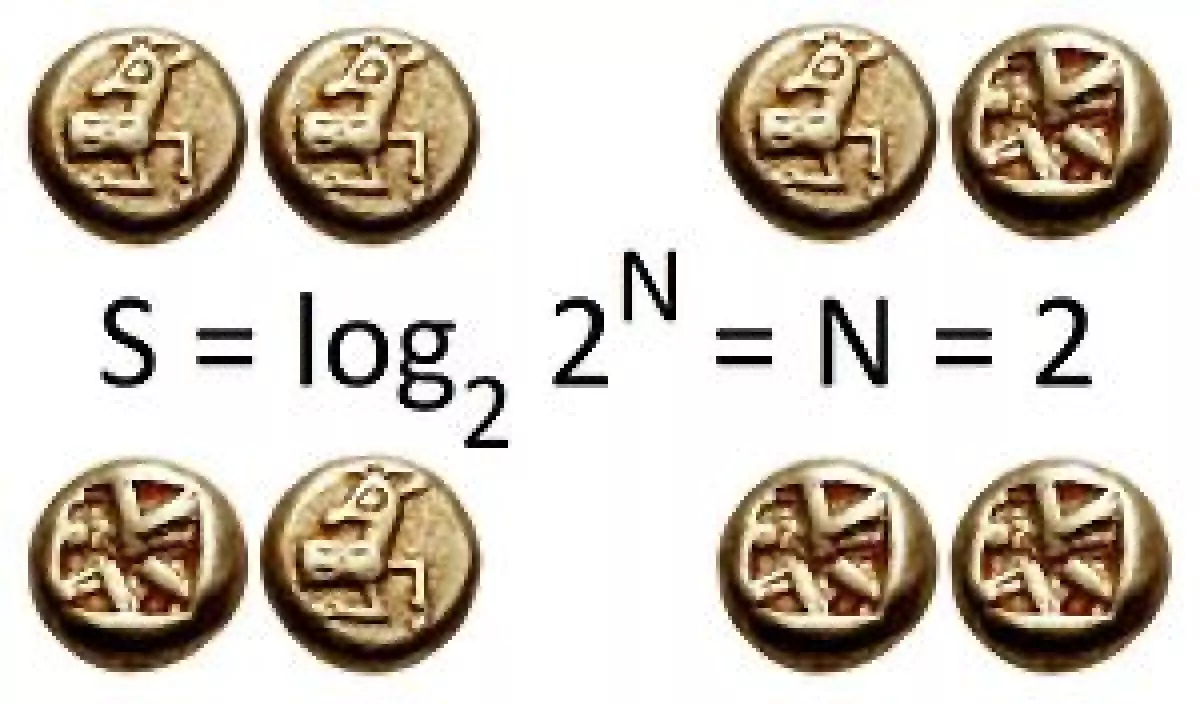
Why Should You Care About Information Entropy?
Whether you're a tech enthusiast or just curious about how things work, understanding entropy gives you a peek behind the digital curtain. Here's why it matters:
-
Data Compression: Ever wondered how we squeeze massive files into zip folders? Entropy! By understanding the predictability (or lack thereof) in data, we can represent it more efficiently.
-
Communication: From sending messages to streaming movies, we rely on transmitting data cleanly. Entropy helps us figure out the limits of what's possible, even with noisy connections.
-
Machine Learning: Yes, even algorithms use entropy! It helps them make decisions with uncertain information, like classifying images or predicting what you'll type next.
From Surprise to Equations: Digging a Little Deeper
Mathematically, entropy is all about probabilities. The less likely an event, the higher its information content. Think of it like this:
-
Certain Event: The sun will rise tomorrow. (Probability ≈ 1, Entropy ≈ 0 – no surprise here!)
-
Unlikely Event: Winning the lottery. (Probability ≈ 0, Entropy is high – now that's news!)
Shannon gave us a nifty formula to calculate this:
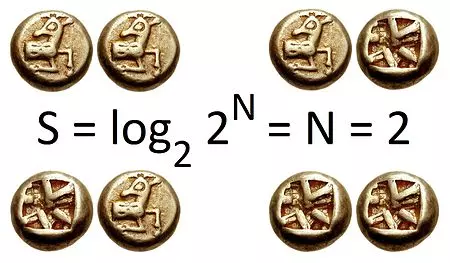
Don't let the symbols scare you! This formula just takes the probability of each possible outcome, throws in a logarithm (which measures how surprising something is), and averages the results.
The Beauty of Entropy: Connections Everywhere!
What's truly fascinating is how entropy pops up in fields beyond just information theory:
-
Thermodynamics: This branch of physics uses entropy to describe the disorder or randomness of systems. A messy room, for instance, has higher entropy than a tidy one.
-
Linguistics: Remember how predictable English text is? Languages have their own kind of entropy, influencing how we communicate and even how languages evolve over time.
So there you have it – entropy in a nutshell! It's a concept that bridges the gap between information, surprise, and the very fabric of how we make sense of the world.











